




Collection along with its minions List, Set, BitString, OctetString, Stack, String, and Dictionary.
This chapter takes a close look at Collection and its subclasses. You'll learn how to derive classes from the Collection class families, and then see how to instantiate those classes to create collections, lists, sets, stacks, and other Collection objects. A look at each class's features shows you how to manipulate these objects--how to modify and examine their contents and how to convert them to objects of other types.
Collection and other classes described in this chapter. All class families have double square braces following their name ([]). The mix-in superclass Compared is preceded by <: because the superclass can be specified as Compared or either of its two subclasses--depending on how a class is derived from the class family Collection. (You'll read about the details of Collection derivation later in this chapter.) All classes and class families described in this chapter are in boldface.Object
* Collection[] (<:Compared)
* * List[] (Ordered)
* * * BitString
* * * OctetString
* * * Stack[]
* * * String (Cased)
* * Set[] (Verified)
* * * Dictionary[]
Collection defines features that are inherited by seven other predefined Telescript classes and class families--the collection classes.A Collection object is an unordered group of objects. The objects are the collection's items; you provide them (or none, if you prefer) when you initialize the object. Once a collection exists, you can use its operations to examine and modify it--check to see how many items there are, add a new item, delete an existing item, check to see if a given item is included in the collection, or take any number of other possible collection actions.
A List object inherits the features of Collection and adds a key aspect: it orders its items so they each have a numbered position--1, 2, 3, 4, and so on. It adds new operations that can add, delete, and move items within the list; operations that can retrieve an item from a specified position; and operations that can add sublists (other lists of items) to the list.
List has four built-in subclasses. BitString creates objects that store lists of 1s and 0s--in other words, that store binary data. OctetString creates objects that store strings of octets; you can think of an octet string as a stream of bytes. Stack creates a LIFO (Last In, First Out) stack where you can push, pop, swap, and roll items. And String creates objects that store lists of characters. String isn't discussed in this chapter; you can read about it in the next chapter, where it plays an integral role in the text-handling capabilities of the Telescript environment.
Set is the second of Collection's two built-in predefined subclasses. Unlike List, it does not impose order on its items. Instead, it ensures that each of its items is unique--that no two items in the set match. A Set object, then, is a collection of unique items that may occur in any order. Set operations allow you to work with one set against another: to create a union of the two sets, to create the intersection of the two sets, to create a set that is the difference of one set from the second set.
Set has one built-in subclass: Dictionary. Dictionary treats each of its items as a key. It pairs each key with a value--that is, another object (you can specify the type of object allowed). A Dictionary object, then, contains key-value pairs. Dictionary's operations allow you to provide a key and retrieve the value associated with that key. The operations also allow you to add and drop key-value pairs and modify the dictionary in other ways. Dictionaries are commonly used in the Telescript environment as an unordered lookup table. The dictionary groups together a set of values (whatever objects are provided in initialization and later modification); each value has a key used for retrieval. The characteristics that Dictionary inherits from Set ensure that each key is unique.
Object
* Iterator[]
* Exception
* * ProgrammingException
* * * CollectionException
* * * * KeyInvalid
* * * * PositionInvalid
* * * * StackDepleted
Compared
* Equal
* Same
Ordered
Verified
Iterator defines an object that can produce a reference to an item in a collection each time it's requested to do so. An iterator is returned by the Collection operation iterator; you can use the iterator to step through the collection's items. The iterator allows you to examine the contents of a collection.
CollectionException is a sub-subclass of Exception; it defines three subclasses--KeyInvalid, PositionInvalid, and StackDepleted--that are thrown by operations of Collection and its subclasses.
Compared is a mix-in class that defines how two objects are considered matching objects. Its two subclasses--Equal and Same--use different criteria to determine how objects match. One of these three mix-ins--Compared, Equal, or Same--is chosen as the mix-in superclass for Collection when you derive a class from it. The mix-in chosen determines how matching works in any operations that depend on matching.
Ordered is a mix-in class used as a superclass for List. As you learned in Chapter 5, it's also used extensively with primitives such as numbers, bits, and characters, where it determines the order relationship between two objects--before, equal to, after, or unordered. By mixing Ordered into the List definition, it allows two lists to be ordered so one list can be before, equal to, or after another.
Verified is a mix-in class used as a superclass of Set. It's used to help determine if a set is internally inconsistent--that is, outside influences (discussed later in this chapter) have created matching items in the set.
If you look at the first class tree presented in this chapter, you'll notice that the class family Collection has two subclasses that are also class families: List and Set. List has in turn some subclasses that are flavor classes, and one subclass that is a class family. To see how this works, consider the nature of a class family.
A class family, as you'll recall from previous chapters, is a class-producing function that specifies classes within itself using formal parameters (formals). When these formals are satisfied by actual parameters (actuals), the class family derives a class. A class family itself can't be directly instantiated; you must first derive a class from the family and then instantiate the derived class.
List and the class BitString (both shown in the previous hierarchy). BitString is really a subclass of the derived class List[Bit, Equal]. The class hierarchy doesn't show the derived class, but if you look up BitString in the class reference documentation, you'll see in the class signature that List[Bit, Equal] is the primary superclass of BitString. In other words, BitString's class definition defines the derived class List[Bit, Equal] as its primary superclass.Stack shown in the class tree. If you look at its definition in the class reference documentation, you'll see that Stack, like BitString, specifies a derived class of List as its primary superclass. But--as a class family--Stack can use a formal anywhere in its definition where it specifies a class. One place you'll always find classes in a class definition is in its superclass specification. In this case, Stack defines its own formals Item and Match. It then uses those formals to specify its superclass, which is a class derived from the class family List. The formals are supplied as the actuals of List in this way: List[Item, Match].
The effect is that Stack's inheritance isn't determined until you derive a class from Stack. When you supply actuals for Stack, those actuals are passed on as actuals for List to derive a primary superclass for Stack.
Stack requires actuals for its formals Item and Match. If you provide the actuals Number and Equal, you create the derived class Stack[Number, Equal]. This derived class uses your actuals to satisfy its formals wherever they occur in the class family definition. Two of those formal occurrences are in the inheritance specification for the class family. These formals specify which derived List class will be the immediate superclass of Stack. When they're satisfied, they specify the derived class List[Number, Equal] as the immediate superclass of Stack[Number, Equal].
As a further example, if you provide the actuals Primitive and Same for Stack, you create the derived class Stack[Primitive, Same]. It has the immediate superclass List[Primitive, Same] because the actuals are used to define the immediate superclass.
In cases of inheritance like the one just described, it may help to think of the formals of a subclass family (like Stack) as "percolating formals." They are linked directly to the formals of the superclass family, so any actuals you supply percolate up to derive a class from the superclass family.
Percolating formals can go up many levels, as is the case for Stack. When you supply actuals for the formals Item and Match, those actuals are passed up to derive a class from the superclass family List. The derived List class, in turn, passes those actuals up to its superclass family Collection to derive a class there. So when you derive the class Stack[Number, Equal], your actuals Number and Equal are passed on to derive the superclass List[Number, Equal] and the super-superclass Collection[Number, Equal].
If you want all the gnarly and incestuous details of inheritance and class families, you'll find them in Chapter <<<yet to be written>>>, which gives full information on defining your own class families.
Collection is the root of all collection classes. It's a concrete and unsealed class family, so you can derive classes and instantiate them to create Collection objects. You can also define your own Collection subclasses.
As you read earlier, Collection defines an object that is an unordered group of objects, the collection's items. The number of items in the collection determines the collection's length. For example, a collection that includes 25 items has a length of 25; a collection with no items has a length of 0. A collection's length is unbounded; a collection can have as many items as available computing resources will permit.
It's important to remember that a collection's items are unordered. None of a collection's operations depends on order when finding, retrieving, and adding items to the collection. In fact, if you iterate through a collection's items, you can't be assured that the items will be iterated in the same order each time. If you want ordered items, you can work with List, a subclass of Collection.
Because Collection is a class family, you must derive a class from it before you can instantiate a collection. To do so, you must satisfy two formals: Item, which constrains the type of items that may be included in the collection; and Match, which specifies the mix-in superclass that determines how the collection matches items. If you use Collection as a class name without providing actuals, the default derived class is Collection[Object, Compared].
Item. Any items you add to the collection must be a member of the specified class. If, for example, you specify Number as an actual for Item, the collection can include any items that are integers or real numbers. If you use Object as the actual for Item, any type of object may be included in the collection. Object is Collection's default actual, so a default collection can include any type of object.Compared mix-in: compare. compare accepts two objects as its arguments and compares them to determine their relationship: equal or unordered. Any two objects that are equal are considered a match; any unordered objects are not a match.
(Don't confuse the mix-in Compared with the mix-in Ordered that you read about in Chapter 5. Ordered allows you to determine a relationship between two ordered objects such as most primitives: equal to, before, after, or unordered. Compared lets you determine a relationship between two objects whether or not they're ordered objects, and--as it's implemented--determines only two relationships: equal or unordered.)
The Telescript language uses two kinds of matching: copy-equal matching and same-object matching. In copy-equal matching, two objects are considered equal (a match) if they are copy equal--that is, one object could have been created by calling the copy operation on the other object. (copy is an operation inherited by all objects from the root class Object. It's discussed in Chapter 5 and in greater detail in Chapter <<<yet to be written>>>.)
In same-object matching, two objects are considered equal (a match) only if they are references to the same object. If, for example, the variable tempos and the variable speeds both refer to the same collection, tempos and speeds would be considered a same-object match. Same-object matching is much more restrictive in its definition of matching objects than copy-equal matching. Two objects that may be copy equal aren't necessarily a same-object match; two objects that are a same-object match, however, must always be copy equal.
Keep in mind, when considering same-object matching, that Telescript primitives (numbers, characters, etc.) are the same object if they have the same value. In other words, the integer 5 used in one variable assignment is the same object as the integer 5 used in another variable assignment, even if you might think of them as different instances. The Telescript engine, for economy, has a single instance of 5 that it uses for both cases of 5.
Collection's Match formal specifies how matching is determined within a collection. The formal is defined to accept Compared or either of its subclasses Equal or Same. The class supplied as the actual becomes the mix-in superclass of the derived class. So if, for example, you derive a Collection class by specifying Equal as the Match actual, the class's flavor superclass is Object and its mix-in superclass is Equal. (The flavor superclass is always Object no matter what mix-in superclass is specified.)
The three possible Match mix-in classes each have a definition of how the relationship "equal" is determined when the operation compare is called.
Compared is the superclass of both Equal and Same; it defines and implements the compare operation available in all three mix-in classes. compare, as implemented by Compared, takes two objects as arguments and returns their relationship:
equal.
unordered.
Equal has the same interface and implementation as Compared. When you use its compare operation to compare two objects, it returns equal for copy equal objects and unordered for object that aren't copy equal. There's no practical difference between specifying Equal or Compared as the Match actual for a collection. Both mix-ins set the collection to consider copy-equal objects as matching.
Equal is the most commonly used class for Match--so most derived collection classes are defined to consider copy-equal objects as matching.
Same has the same interface as Compared, but has its own implementation of the operation compare. This implementation is almost identical to Compared and Equal's implementation with one important difference: it returns the identifier equal for two objects only if those objects are references to the same object. It returns the identifier unordered for any two objects that aren't references to the same object.
The functional difference is that if you derive a collection class using the mix-in Same, matches are made using same-object matching, not the copy-equal matching used for classes derived using Equal or Compared.
Collection by supplying actuals for Item and Match and then provide initialization arguments. This all takes place in an initialization statement.
Collection's class signature (shown in the class reference documentation) shows you the formals and how they must be satisfied:
Collection: interface[Item: Class; Match: Class<:Compared]In other words,
Item can be satisfied with any class, while Match must be satisfied with Compared or either of its two subclasses, Equal and Same--a topic you just read about.
The initialize operation's signature shows you the required initialization arguments:
initialize: op (items: Item ...);The argument
Items is followed by an ellipsis (...), so this means you can supply as many arguments as you wish (or none if you don't want to supply any arguments). The constraint for items is given as Item, which--as you'll remember--is one of the formals for Collection. Whatever actual you supply for Item is the constraint for the argument items. In other words, if you derive the class Collection[Number, Equal], the formal Item is satisfied by the actual Number. This means that the constraint for items is Number.
Each of the items arguments you supply for initialization becomes an item of the collection. Consider this example:
Collection[Number, Equal](5, 3.78, 9375, 0.05760);This initialization statement derives the class
Collection[Number, Equal], which can only include items that are members of the Number class and that considers objects matching if they're copy equal. The four arguments that follow are all items of the collection. Once the collection is initialized, you have a collection with the items you specified as initialization arguments.Collection offers three operations that let you modify a collection:
include accepts a single object as an argument; it adds that object to the collection as an item.
exclude accepts a single object as an argument; it finds an item that matches the argument, removes it from the collection, and returns it. If the collection contains more than one matching item, exclude finds, removes, and returns the first match it finds. Because a collection is unordered, you can't be sure which of the matching items it will find.
clear accepts no arguments. When it executes, it removes all items from the collection.
Collection also offers features that you can use to examine the length and contents of a collection:
length, a read-only attribute, contains the collection's length (an integer value). Use it when you want to provide the number of items in a collection as a value.
examine accepts a single object as an argument; it finds an item that matches the argument and returns it. If the collection contains more than one matching item, examine finds and returns the first match it finds. You can't be sure which of the matching items it will be. examine works quite a bit like exclude, but it doesn't remove the found item from the collection--it leaves the item in place.
iterator accepts no arguments and returns an iterator when executed. You can use the iterator to step through the items of the collection.
Iterator. An iterator holds a reference to a corresponding collection, and can produce references to each of the collection's items. Like a collection, an iterator is created as an instance of a class derived from a class family. The class family Iterator has a single formal to satisfy: Item. This formal has the same meaning here as it does in the class family Collection; it constrains the type of items to which the iterator may refer. The derived class Iterator[Primitive], for example, defines an iterator that may only refer to items that are primitives.
Iterator is an abstract class family; you can't create instances of it yourself, but the Telescript engine can--and does--whenever you call iterator on a collection. The iterator returned is constrained to the same type of items as the collection from which it was returned. The iterator has a reference to the collection for which it was created, and can produce a reference to each of the collection's items. In this way the iterator can refer to the same group of items as the collection.
An iterator offers three attributes: current, next, and isDone. You use these attributes to examine a collection's items. The first time you use the next attribute, it returns one of the collection's items. The next time you use next, it returns another of the collection's items. In subsequent uses of next, it returns the rest of the collection's items without repeating any item. When it has returned all of the items in the collection it returns nil.
If you want to repeat access to a collection item, use the current attribute. It returns the last item produced by the next attribute. You can use it again and again without affecting the sequence of iteration used by next.
You can check the isDone attribute at any time to see if the iterator has returned all of a collection's items. Its value is true if that's the case, false if not. This is particularly useful if the next operation has returned nil--the nil could either be an item in the collection, or it could mean that the iterator has returned all the items in the collection. isDone tells which case is true.
When an iterator is done, its current and next attributes will return only nil. If you need to iterate through a collection's items once again, you should discard the iterator, call iterator on the collection again, and work with a new iterator.
It's important to note that an iterator is used strictly for examination. Its items are references to existing items in a collection, and using an iterator has no effect on the collection from which it sprang. Discarding an iterator has no effect on the collection.
It's also important to note that--because a collection is an unordered group of items--you can't depend on iterators to iterate through a collection's items in the same order each time you use them. (If you use an iterator for a list, though, it does step through items in ascending order.)
copy is an operation inherited from the class Object; Collection overrides it so that the operation considers each item in the collection as a property of the collection. This means that when you call copy on a collection, you create a copy of the collection that contains items that are copies of the original items.
shallowCopy, a Collection operation, copies as copy does with one exception: it doesn't create copies of each item for the copied collection. It simply uses the same group of items for the copied collection. This means that both collections have references to the same group of items. You can use a shallow copy in place of an iterator if you want access to the items as you examine them.
asList. It returns a list whose items are those of the collection. Because a collection is an unordered group of items, you can't be sure what the order of the items in the returned list will be.
1 do{
2 /* Initialize a collection and modify it. */
3 grabbag: = Collection(1, 'A', 4.657, 'A', 'z');
4 "The collection after initialization:".dump();
5 grabbag.dump();
6 grabbag.exclude('A');
7 "After an A has been excluded:".dump();
8 grabbag.dump();
9 grabbag.include(6);
10 "After a 6 has been included:".dump();
11 grabbag.dump();
12 /* Create an iterator for the collection "grabbag", then iterate
13 through its items in a while loop that tests the iterator's
14 isDone attribute. */
15 look: = grabbag.iterator();
16 "An iterator going through the items of the collection:".dump();
17 while !look.isDone {
18 look.next.dump()
19 };
20 "There are no more items to be iterated.".dump();
21 }
When you execute the program, you get the following results:
String: <The collection after initialization:>
Collection: <5 elements>
Integer: <1>
Real: <4.657>
Character: <65(A)>
Character: <65(A)>
Character: <122(z)>
String: <After an A has been excluded:>
Collection: <4 elements>
Integer: <1>
Real: <4.657>
Character: <65(A)>
Character: <122(z)>
String: <After a 6 has been included:>
Collection: <5 elements>
Integer: <1>
Real: <4.657>
Integer: <6>
Character: <65(A)>
Character: <122(z)>
String: <An iterator going through the items of the collection:>
Integer: <1>
Real: <4.657>
Integer: <6>
Character: <65(A)>
Character: <122(z)>
String: <There are no more items to be iterated.>
The program is pretty straightforward. It creates a collection named grabbag and initializes it with five items, then dumps the collection so you can see its contents. Notice that two of the items are duplicates: the "A" characters. Notice also that no actuals were specified in the initialization, which derives the class Collection[Object, Compared] (the default derivation) from the Collection class family.Line 6 excludes an "A" from the collection; line 9 includes a 6. A dump of the collection after each action shows the new items.
In line 15, the operation iterator is called on the collection to create an iterator named look. A while loop checks the iterator's isDone attribute; as long as it's false, the loop steps through the items of the iterator (which are the collection's items). When there are no more items to step through, isDone becomes true, and the loop ends.
List class family adds an important element to Collection: order. Each of the items in a list is associated with an integer that is the item's position. Positions start at a value of 1 and extend to a value that equals the length of the list. Position is important when working with a list; you use it to specify items and ranges of items within a list. You may also receive the position of an item as the result of an operation. (If you program frequently in C, be sure to remember that Telescript lists start with position 1, not with position 0 as C arrays do.)
The List class family, like Collection, has two formals: Item and Match. These formals have the same meaning they do in the Collection class family, and are, in fact, "percolating formals." The actuals you provide to derive a List class are used as actuals to derive a Collection superclass.
List's definition also specifies a mix-in superclass--Ordered--that allows two lists to be compared and their relationship evaluated. One list may be before, after, equal to, or unordered in relation to the other list.
List by supplying actuals for Item and Match. You then provide initialization arguments. You do both these steps in an initialization statement that looks like the initialization statement for a collection. The actuals you supply have the same constraints as the actuals for Collection. And you supply variable arguments for initialization just as you do when initializing a collection. All the arguments you supply become items of the newly initialized list. The only difference is that the order of the initialization arguments is important: the order of the arguments becomes the order of the items in the list. The order of a list's items determines each item's position in the list.add operation).Collection that it can use to work with single items: include and exclude. Both of these operations have been specialized for the class family List; they take into account the fact that the items of a list are ordered. If you use include to add an item to a list, the item appears at the end of the list. And if you use exclude to remove an item from a list, the positions of all items following the removed item are decreased by 1 so there's no gap in the position numbering.
List defines five of its own operations for working with single items:
add accepts a position and an item as arguments. It adds the new item to the list at the specified position and increases by 1 the position of any items following.
drop accepts a position as an argument. It removes the item at that position and decreases the position of any items following by 1.
set accepts a position and an item as an argument. It uses the new item to replace the item that already exists at that position in the list. If you specify a position of length + 1, it appends the item to the list without replacing any existing items.
reposition accepts two positions as arguments. It moves the item at the first position into the second position, then readjusts the positions of the items between the two positions as necessary.
transpose accepts two positions as arguments. It interchanges the two items at these locations so the item at position one is now at position two and the item at position two is now at position one.
set operation on any class that defines set with the required signature. This syntax works on an instance of List or any of its subclasses. The syntax is an assignment expression that takes this form:
<object>[<position>] = <item>Using this syntax makes setting an item of a list feel like an assignment. This expression, for example,
scores[5] = 235sets the fifth item of the list
scores to a value of 235. The expression is equivalent to this feature expression:
scores.set(5, 235)
List defines two operations that work with lists and sublists. (A sublist is a range of zero or more items within a list.) To specify a sublist within a list, you provide two positions: the starting position and the ending position. The starting position is the position of the first item in the sublist; the ending position is the position of the item following the last item in the sublist (which is length + 1 if the last item of the sublist is the last item of the list). To put it mathematically, the sublist includes items whose positions are in the interval [start, end).Most sublist specifications have an ending position that is larger than the the starting position. Anytime this is the case, the sublist has one or more items. For example, a sublist with starting and ending positions of 3 and 7 specifies items 3-6, a total of four items. And a sublist with the starting and ending positions of 7 and 8 specifies item 7, a total of one item.
You can also specify a sublist whose starting and ending positions are equal. This sublist contains no items and is located just before the start position. In other words, equal starting and ending positions specify a single position that has no items. This is different than the position you specify for a single item because it falls between items and not on an item. For example, if you specify the position 5, you specify item 5 in the list. If you specify the sublist 5,5, you specify the position between item 4 and 5--but you don't specify any item in the list.
A sublist with no items is an important tool when you use the splice operation (described later) because it allows you to specify a position between two items when you insert one list into a second list. If you want to append the list, you can specify the substring length+1, length+1 which specifies the position just after the last item in the list. And if you want to prepend the list, you can specify the substring 1,1 which specifies the starting position just before the first item in the list.
When you specify a sublist, note that it's illegal to use starting and ending positions that are less than 1 or greater than length + 1. It's also illegal to specify a sublist whose ending position is less than its starting position. You can, if you want, use nil as the starting or ending position of a sublist. Nil in the starting position specifies the position 1. Nil in the ending position specifies the position length + 1. This means that the substring specified nil, nil defines all the items from the first item of the list to the last item of the list, inclusive--in other words, the whole list.
List's two operations that work with lists and sublists are these:
append accepts a list as an argument. It appends the items in that list to the end of the responding list.
splice accepts two positions and a list as arguments. The two positions define a sublist within the responding list. The operation removes the items in the specified sublist and modifies the positions of the remaining items to close up the gap. The operation then inserts the argument list into the responder list just before the first position, modifying the positions of the items that follow to accommodate the inserted items. The operation returns a new list made up of the items removed from the responder list.
splice as an operation that can snip out a part of a list and return it to you, splice in a new list of items to a list, or do both simultaneously. You can supply a nil as the list argument if you wish, which allows you to remove a sublist from a list without inserting new items. Or you can use the same position for both position arguments to insert a new list into the responding list without removing any existing items.List inherits examination features from Collection: the length attribute and the operations examine, iterator, and shallowCopy. iterator has been specialized so the iterator it returns iterates through the list's items in ascending order from position 1.
List also provides two examination operations of its own:
find accepts a position and an item as arguments. It looks for a match for the item, starting at the specified position and working up through the positions until it find the first possible match. It returns the position of the matching item in the list.
get accepts a position as its argument. It returns the item at that position in the list.
get, like set, through a special syntax that may be used on any instance of List or its subclasses. The syntax is an expression that takes this form:
<object>[<position>]It evaluates to the value of the item at the specified position. This expression, for example,
scores[5]gets the fifth item of the list
scores. The expression evaluates to the value of that fifth item. It's equivalent to this feature expression:
scores.get(5)
List's mix-in superclass Ordered adds the operations maximum, minimum, and order to a list. These operations determine and act on the order relationship between two objects. List specializes the order operation so that all three oiperations can make sense of lists, which usually have multiple items. Here's how the operations decide if one list is before, after, equal to, or unordered in relationship to a second list:The items of one list are compared one by one, in order, with the items of the second list. Comparison starts with position 1. If the two items there are equal, the comparison moves to the next position, and continues on to successive positions until an unequal pair of items is found. The order of that unequal pair of compared items determines the order of the two lists. If, for example, you compare a first list of (4, 2, 7, 5, 9) to a second list of (4, 2, 6), the lists are equal until position three, where the 7 of the first list is after the 6 of the second list. This means that the first list is after (greater than) the second list.
If a shorter list has items that are equal to the corresponding items of a longer list, then the shorter list is before the longer list. For example, the list (4, 2, 7) comes before the list (4, 2, 7, 5, 9).
If two lists have equal lengths and contain items that are equal to each other and are in the same order, the two lists are equal. For example, the list (4, 2, 7, 5) is equal to the list (4, 2, 7, 5).
do{
/* Initialize a list and modify it in different ways. */
letters: = List[Character, Equal]
('A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J');
"The list after initialization:".dump();
letters.dump();
letters.add(5, 'X');
"After an X has been added at position 5:".dump();
letters.dump();
letters.drop(8);
"After the item at position 8 has been dropped:".dump();
letters.dump();
letters[5] = 'Z';
"After item 5 has been set to Z:".dump();
letters.dump();
letters.reposition(5, 7);
"After item 5 has been repositioned to position 7:".dump();
letters.dump();
letters.transpose(1, letters.length);
"After the first and last items have been transposed:".dump();
letters.dump();
}
When you execute the program, you get the following results:
String: <The list after initialization:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
Character: <71(G)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After an X has been added at position 5:>
List: <11 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <88(X)>
Character: <69(E)>
Character: <70(F)>
Character: <71(G)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After the item at position 8 has been dropped:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <88(X)>
Character: <69(E)>
Character: <70(F)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After item 5 has been set to Z:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <90(Z)>
Character: <69(E)>
Character: <70(F)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After item 5 has been repositioned to position 7:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
Character: <90(Z)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After the first and last items have been transposed:>
List: <10 elements>
Character: <74(J)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
Character: <90(Z)>
Character: <72(H)>
Character: <73(I)>
Character: <65(A)>
As you can see, the program created a list of characters (in alphabetical order so you can more easily see list changes), then modified the list by working with individual items.The following short program works with substrings:
1 do{
2 /* Initialize a list and modify it using substrings. */
3 letters: = List[Character, Equal]
4 ('A', 'B', 'C', 'D', 'E', 'F', 'G');
5 "The list after initialization:".dump();
6 letters.dump();
7 letters.append(List[Character, Equal]('H', 'I', 'J'));
8 "After the string HIJ has been appended:".dump();
9 letters.dump();
10 removed: = letters.splice(4, 7, List[Character, Equal]
11 ('X', 'Y', 'Z'));
12 "After the substring XYZ has been spliced into
13 position 4-6:".dump();
14 letters.dump();
15 "This substring was removed by the splice:".dump();
16 removed.dump();
17 }
When you execute the program, you get the following results:
String: <The list after initialization:>
List: <7 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
Character: <71(G)>
String: <After the string HIJ has been appended:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
Character: <71(G)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <After the substring XYZ has been spliced into
position 4-6:>
List: <10 elements>
Character: <65(A)>
Character: <66(B)>
Character: <67(C)>
Character: <88(X)>
Character: <89(Y)>
Character: <90(Z)>
Character: <71(G)>
Character: <72(H)>
Character: <73(I)>
Character: <74(J)>
String: <This substring was removed by the splice:>
List: <3 elements>
Character: <68(D)>
Character: <69(E)>
Character: <70(F)>
A few things to notice in this last program: the list arguments supplied in lines 7 and line 10 are of the same derived class (List[Character, Equal]) as the class being modified. That's because the compiler won't accept substrings of a different derived class than that of the modified string. In line 10, the positions 4 and 7 are used to specify the substring in positions 4 through 6; remember that the end of a substring is always specified with the position following the last item of the substring.List has four predefined subclasses: BitString, OctetString, Stack, and String. String is discussed in the next chapter. Let's look at the other three subclasses now.BitString is a subclass of the derived class List[Bit, Equal]--which means that it's a list designed to include bits as items. It inherits all the features of List, and adds a few new twists of its own.%"), follows with zeroes and ones, and ends with another double quote ("). For example, the bit-string literal %"10011" creates a bit string whose items are %1, %0, %0, %1, and %1.
It's important to note that when you use a literal to create a bit string, the bit string returned is a protected bit string--that is, it can't be modified. Protection is an advanced topic covered in later chapters. For now, it's enough to know that you can't modify the contents of a bit string literal or use the bit string as an argument for an operation that requires an unprotected bit string (whose constraint is preceded by the keyword unprotected). You must initialize a bit string instead, which returns an unprotected bit string. Or you can copy the string literal and use the copy as the argument.
%1, %0, %0, %1, %1, for example), you can supply one or more bit-string literals or variables, or you can combine bits and bit strings as arguments. Combining allows you to concatenate existing bits and bit strings into a new bit string. For example, this constructor expression
BitString(%1, %"10010", %0, %1, %"10101010")constructs the new bit string
%"1100100110101010".BitString specializes its inherited operation order so that when two bit strings are compared, the shorter of the two bit strings is treated as though it had enough zero bits prepended to it to equal the length of the longer bit string. This means, for example, that the bit string 1011 is before 101010 because 001011 is compared to 101110 to determine their order. (If the two bit strings were compared simply as lists of bits, 1011 would be after 101010 because the fourth bit of 1011 is greater than the fourth bit of 101010.)BitString provides its own conversion operation: asOctetString. The operation returns an octet string that is the hexadecimal equivalent of the binary value contained by the bit string.OctetString is a subclass of the derived class List[Octet, Equal]. It's a list designed to include octets (hexadecimal values) as its items. It inherits all the features of List and adds features of its own. We'll discuss all of them except the operation decode, which is an advanced feature discussed in Chapter <<<yet to be written>>>, where you learn about encoding and decoding.$"), follows with pairs of hexadecimal digits (0-f or 0-F), and ends with another double quote ("). For example, the octet-string literal $"f4401dba" creates an octet string whose items are $f4, $40, $1d, and $ba.An octet-string literal, like a bit-string literal, returns a protected octet string that you can't modify. If you need an unprotected octet string that you can modify or use as an unprotected argument for an operation, initialize an octet string to create an unprotected octet string.
$F4, $40, $1D, $BA, for example), you can supply one or more octet-string literals or variables, or you can combine octets and octets strings as arguments. Combining allows you to concatenate existing octets and octet strings into a new octet string as in the following constructor expression:
OctetString($50, $"df98", $ab, $"f284")The expression constructs the new octet string
$"50df98abf284".OctetString specializes its inherited operation order so that when two octet strings are compared, the shorter of the two octet strings is treated as though it had enough zeroes prepended to it to equal the length of the longer octet string. This means, for example, that the octet string 9d2 is before 2fc3 because 09d2 is before 2fc3.
asBitString returns a bit string whose binary value is equal to the hexadecimal value of the octet string.
asInteger returns an integer whose decimal value is equal to the twos-complement binary value of the octet string. That integer may be positive or negative.
asString returns a string of characters that is the result of interpreting the octet string as if it was an FSS-UTF file. If the octet string doesn't conform to FSS-UTF specifications, the operation returns ConversionUnavailable.
You will probably never have to worry about FSS-UTF specifics in Telescript programming because the operation asOctetString defined by the class String converts a Telescript string into an FSS-UTF octet string, and the operation asString converts the octet string back into the original string of Unicode characters.
Stack is a class family that inherits from the class family List. Stack has two "percolating formals"--Item and Match--that have the same meaning they do in a list. That is, Item constrains the items that may be in the stack, and Match specifies how the stack determines two matching items.
Stack inherits all of List's features without specializing them. It also provides a set of five operations--pop, push, pushItems, roll, and swap--that make a Stack object a last-in, firsts-out (LIFO) stack. The top of the stack is position 1. The bottom of the stack is the highest position available (the length of the stack).
Stack class family by providing actuals for Item and Match; you then provide initialization arguments. The arguments become the items of the stack, arranged in the order in which you provided the arguments. The first initialization argument is at the top of the stack, the last argument is at the bottom.Stack's operations allow you to manipulate a stack in all the traditional ways:
push accepts one item as its argument; it pushes the item onto the top of the stack.
pushItems accepts a list as its argument; it pushes the list onto the top of the stack. The first item of the argument list is the highest item in the stack.
pop accepts no arguments; it pops the top item off the stack and returns it as a result.
swap accepts no arguments; it switches the positions of the items at positions 1 and 2.
roll accepts two integers as its arguments; it rolls the items at the top of the stack according to the values passed in the arguments. The second argument specifies how many items to roll--that is, how many items from the top of the stack are affected by the roll. The first argument specifies how many positions the rolled items are moved. If this argument is a positive value, the affected items are rolled toward the top of the stack; if negative, they roll toward the bottom of the stack. Because this is a roll, any item that gets moved beyond the top position of the affected items is jumped to the bottom position of the affected items; any item that gets moved beyond the bottom position is jumped to the top position. Figure 8-1 shows how roll affects a stack.
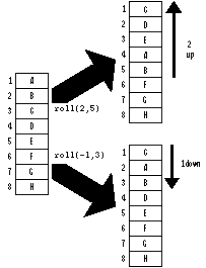
Figure 9-1 : The stack on the left is the original stack. Its top five items are rolled two positions forward in the upper right stack. Its top three items are rolled one position backward in the lower right stack.
do{
/* Initialize a bit string and convert it. */
bitValue: = BitString(%"10010101100111001", %0, %1);
"The bit string after initialization:".dump();
bitValue.dump();
octetValue: = bitValue.asOctetString();
"After converting the bit string to an octet string:".dump();
octetValue.dump();
"The octet string as an integer:".dump();
octetValue.asInteger().dump();
/* Initialize a stack and manipulate it. */
filo: = Stack[Integer, Equal](46, 37, 25, 13, 2);
"The stack after initialization:".dump();
filo.dump();
filo.pushItems(List[Integer, Equal](354, 265, 100));
"The stack after pushing a list of three items:".dump();
filo.dump();
filo.roll(2,5);
"The stack after rolling the top 5 items 2 places:".dump();
filo.dump();
}
When you execute the program, you get the following results. Note that dump lists the items of a stack from bottom to top so a stack printout looks inverted. You have to turn your perspective on its head to see what's going on with the stacks.
String: <The bit string after initialization:>
BitString: <1001010110011100101>
String: <After converting the bit string to an octet string:>
OctetString: <959C>
String: <The octet string as an integer:>
Integer: <38300>
String: <The stack after initialization:>
Stack: <5 elements>
Integer: <2>
Integer: <13>
Integer: <25>
Integer: <37>
Integer: <46>
String: <The stack after pushing a list of three items:>
Stack: <8 elements>
Integer: <2>
Integer: <13>
Integer: <25>
Integer: <37>
Integer: <46>
Integer: <100>
Integer: <265>
Integer: <354>
String: <The stack after rolling the top 5 items 2 places:>
Stack: <8 elements>
Integer: <2>
Integer: <13>
Integer: <25>
Integer: <265>
Integer: <354>
Integer: <37>
Integer: <46>
Integer: <100>
The program initializes a bit string named bitValue, converts it to an octet value that it uses to create an octet string named octetValue, then converts the octet string to an integer value. Notice that the initialization arguments for the bit string contain both a bit-string literal and individual bits; they're concatenated to create a single bit string. The program then creates a five-item stack, pushes on a list of three more items, and rolls the top five items two places.Set, like List, is one of the two built-in immediate subclass families of Collection. Set brings the characteristic of uniqueness to the unordered items of a collection--it checks its items to make sure that no one item matches any other item in the set.
Set's features are designed to avoid duplicate items by checking any new item added to the set against existing items. If the set finds a match, it excludes the existing item from the set before including the new item.
The uniqueness of items in a set isn't always guaranteed. It can be compromised when an item is changed by an external action--that is, an action that does not take place through the features of the set. For example, an object outside the set may have an independent reference to an item in the set. That outside object may change the value of the item without the knowledge of the set and may--by chance or design--change the set item so that it matches another set item. If that happens, the set is said to be internally inconsistent. A set whose items are all unique is said to be internally consistent. You can, as you'll see, guard against internal inconsistency.
The Set class family has two formals that percolate up to Collection: Item and Match. These formals have the same meaning that they do in the Collection class family, and are used to derive a Collection superclass.
Set also has one mix-in superclass: Verified. This class offers an operation--verify--that checks a set's integrity and reports if the set is internally consistent. You can then take actions to fix the integrity or recreate the set.
Item and Match to derive a class. The Item actual sets the class type of items that may be included in the set; the Match actual determines how two items are considered a match. Keep in mind, when setting Match, that if you supply Equal as the match, it creates a much more restrictive set than Same. That's because a set that only considers two items that are the same object as a match doesn't check for copy-equal items. A set defined with Equal will exclude copy-equal items.Once you've supplied actuals, you supply a variable number of arguments for initialization just as you do when initializing a collection--the arguments are a group of objects that become the items of the set. When initializing a set, as when initializing a collection, the order of the object you supply doesn't determine the order of the items in the set because the items are unordered.
There is one important difference between initializing a set and initializing a collection: when you initialize a set, the set ensures that no two of its items match. When a set is initialized, the initialize operation checks each object as it's passed in to become an item in the set. If an object matches an item already in the set, the set item is discarded to make way for the new item. This ensures that a newly initialized set has no matching items--that it's internally consistent. And for this reason, the order of the initialization arguments can make a difference in rare cases.
difference checks every item of the argument set against items of the responder set, and discards every item in the responder that matches. This operation has the effect of turning the responder set into the difference between the argument and responder sets.
intersection discards from the responder set every item that doesn't match an item in the argument set. This operation has the effecgt of turning the responder set into the intersection of the argument and responder sets.
union looks at each of the items in the argument set; if any item isn't matched in the responder set, it's included in the responder set. This operation has the effect of turning the responder set into the union of the argument and responder sets.
Set's mix-in superclass Verified adds the operation verify to a set. The operation accepts no arguments. It's specialized so that when you call it, it returns the boolean true only if the set is internally consistent--in other words, it has no matching items. Use this operation as necessary to confirm the integrity of a set.
do{
/* Initialize four sets and work with them. */
oddSet: = Set[Integer, Equal](3, 5, 7, 9);
oddShortSet: = Set[Integer, Equal](1, 3, 5, 7);
evenSet: = Set[Integer, Equal](4, 6, 8);
mixedSet: = Set[Integer, Equal](1, 2, 3);
oddSet.union(evenSet);
"oddSet (3,5,7,9) after union with (4,6,8):".dump();
oddSet.dump();
oddSet.intersection(oddShortSet);
"oddSet after intersection with (1,3,5,7):".dump();
oddSet.dump();
oddSet.difference(mixedSet);
"oddSet after difference with (1,2,3):".dump();
oddSet.dump();
}
When you execute the program, you get the following results:
String: <oddSet (3,5,7,9) after union with (4,6,8):>
Set: <7 elements>
Integer: <3>
Integer: <5>
Integer: <7>
Integer: <9>
Integer: <4>
Integer: <6>
Integer: <8>
String: <oddSet after intersection with (1,3,5,7):>
Set: <3 elements>
Integer: <3>
Integer: <5>
Integer: <7>
String: <oddSet after difference with (1,2,3):>
Set: <2 elements>
Integer: <5>
Integer: <7>
The program creates four sets. It uses the set oddSet as the responder, using its operations to create a union, an intersection, and a difference with each of the other three sets in turn. Notice that oddSet itself changes after each operation, so the operations have a cumulative effect on oddSet.Dictionary class family is a subclass of the Set class family. It's used primarily to store objects for indexed retrieval. To make this possible, a dictionary uses key-value pairs. Each item of the set is a key, which is an object used to add or request a stored object. Each key is associated with a single value, which is an object stored for retrieval. And each key-value pair stored in a dictionary is an entry.
You should think of a dictionary as a set of key-value pairs (not just items). Whenever you modify a dictionary, you work with key-value pairs. When you use the inherited Collection operations include or exclude, you include or exclude a key-value pair. And whenever you use the inherited Set operations difference, union, and intersection, you add or delete key-value pairs.
It's important to realize that only the keys of a dictionary are considered items, so only the keys are kept unique within the dictionary. The values paired with the keys do not have to be unique. Whenever you include a new key-value pair, the dictionary checks only the key against other keys to enforce the dictionary's internal consistency.
Key, Value, and Match. The actual you supply for Key sets the constraint for objects that can be used as keys within the dictionary. The actual you supply for Value sets the constraint for objects that can be used as values within the dictionary. And the actual you supply for Match sets the way a match is determined within the dictionary. (It works the same as Match does for Collection.)
Key and Match correspond to the formals Item and Match that you find in Set and are, in fact, percolating formals. The actuals you supply for Key and Match are applied to Item and Match in Set to derive a superclass for the dictionary.
As initialization arguments for a dictionary, you supply key-value pairs. This means that you must supply an even number of arguments. Each odd-numbered argument (1, 3, 5, 7, and so on) is a key; each even-numbered argument (2, 4, 6, 8, and so on) is a value. A key is associated with the value that immediately follows to create a key-value pair: argument 1 with argument 2, argument 3 with argument 4, and so on.
When the dictionary is initialized, the key-value pairs are included into the dictionary one at a time starting at the beginning of the arguments. The key of each new pair is checked against the keys of existing pairs. If it matches, the existing pair it matches is excluded from the dictionary before the new pair is included.
difference, intersection, and union are specialized to handle key-value pairs. When you use these operations, any keys you include in or exclude from a dictionary have their values included or excluded with them. The Collection operations include, exclude, and clear are likewise specialized to include or exclude a full key-value pair anytime they include or exclude a key--even though include and exclude accept only a single argument (a key). If include adds a key to a dictionary, a value of nil is provided as the key's corresponding value. (Unless, of course, the value is constrained so it won't accept a nil, in which case the operation throws an exception.)
Dictionary also provides its own modifying operations:
add accepts a key-value pair as arguments. It includes the pair as a new dictionary entry if the key doesn't match the key of any existing entries. If it does match, the pair isn't included, and the operation throws KeyInvalid.
set accepts a key-value pair as arguments. It includes the pair as a new dictionary entry. If the key of the new pair matches the key of an existing dictionary entry, the existing entry is excluded and discarded before the new pair is included.
drop accepts a key as an argument. If it finds an entry whose key matches, it excludes that key-value pair from the dictionary. The operation returns the value of the excluded entry.
rekey accepts two keys as arguments. It looks for an entry key that matches the first argument key. If it finds a match, it discards that key and replaces it with the second argument key, providing a new key for the entry.
transpose accepts two keys as arguments. If it finds matches in the dictionary's entries for both keys, it interchanges those keys so the value of the first entry now has the key of the second entry, and the value of the second entry now has the key of the first entry.
Dictionary's set operation with the same special syntax that's available for setting a list's item. The syntax is an assignment expression that takes this form:
<object>[<key>] = <value>This expression, for example,
tempi["allegro"] = 120sets a dictionary entry whose key is
"allegro" and whose value is 120. The expression is equivalent to this feature expression:
tempi.set("allegro", 120)
Dictionary provides operations you can use to examine a dictionary without modifying its contents:
get accepts a key as an argument. If it finds a matching key in the dictionary's entries, it returns the value associated with the key. If it finds no match, it throws KeyInvalid.
find accepts a value as an argument. If it finds a matching value in the dictionary's entries, it returns the key associated with that entry. If it finds no match, it returns a nil. If there is more than one matching value, find returns the key associated with one of those matching values--it's undefined which match is chosen, so you can't predict which key will be returned.
Dictionary's get operation with special syntax--an expression that takes this form:
<object>[<key>]The expression evaluates to the value associated with the specified key. This expression, for example,
tempi["allegro"]evaluates to the value associated with
"allegro"(which might be 120 if you used the assignment in the last example). The expression is equivalent to this feature expression:
tempi.get("allegro")
1 do{
2 /* Initialize a dictionary, modify it, and examine it. */
3 lookUp: = Dictionary[Character, String, Equal]
4 ('R', "Red", 'G', "Green", 'B', "Blue");
5 "The dictionary after initialization:".dump();
6 lookUp.dump();
7 lookUp.add('C', "Cyan");
8 "The dictionary after adding an entry:".dump();
9 lookUp.dump();
10 lookUp['B'] = "Violet";
11 lookUp['M'] = "Magenta";
12 "The dictionary after setting B and M entries:".dump();
13 lookUp.dump();
14 lookUp.rekey('B', 'V');
15 "The dictionary after rekeying B to V:".dump();
16 lookUp.dump();
17 "The value associated with G:".dump();
18 lookUp['G'].dump();
19 "The key associated with Violet:".dump();
20 lookUp.find("Violet").dump();
21 }
When you execute the program, you get the following results:
String: <The dictionary after initialization:>
Dictionary: <3 elements>
Character: <82(R)> String: <Red>
Character: <71(G)> String: <Green>
Character: <66(B)> String: <Blue>
String: <The dictionary after adding an entry:>
Dictionary: <4 elements>
Character: <82(R)> String: <Red>
Character: <71(G)> String: <Green>
Character: <66(B)> String: <Blue>
Character: <67(C)> String: <Cyan>
String: <The dictionary after setting B and M entries:>
Dictionary: <5 elements>
Character: <82(R)> String: <Red>
Character: <71(G)> String: <Green>
Character: <66(B)> String: <Violet>
Character: <67(C)> String: <Cyan>
Character: <77(M)> String: <Magenta>
String: <The dictionary after rekeying B to V:>
Dictionary: <5 elements>
Character: <82(R)> String: <Red>
Character: <71(G)> String: <Green>
Character: <67(C)> String: <Cyan>
Character: <77(M)> String: <Magenta>
Character: <86(V)> String: <Violet>
String: <The value associated with G:>
String: <Green>
String: <The key associated with Violet:>
Character: <86(V)>
The program creates a dictionary and initializes it with three entries. Notice that the odd-numbered arguments in the initialization statement are the keys, the even-numbered arguments are the values. The program adds an entry, then it sets two entries in lines 10 and 11. Notice that line 10, which sets an entry using a key that already exists, replaces the existing entry B, Blue with B, Violet. Line 11, which sets an entry using a key that doesn't exist, simply adds a new entry to the dictionary.
String, which we'll examine in detail in the next chapter.





Generated with Harlequin WebMaker